Características Gerais do Núcleo
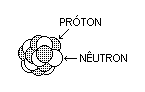
O núcleo atômico é composto de partículas chamadas
núcleons. Existem duas espécies de núcleons: os prótons, com
carga elétrica positiva, e os nêutrons, sem carga elétrica.
Prótons e nêutrons têm spin ½ e obedecem ao princípio de
exclusão de Pauli.
O núcleo do elemento da tabela periódica de número atômico
Z é constituído de Z prótons e N nêutrons. No átomo neutro
correspondente, existem, ao redor desse núcleo, Z elétrons.
A = N + Z é o número de núcleons ou, como também é chamado,
número de massa.
As massas nucleares são convenientemente expressas em
unidades de massa atômica (u). Uma unidade de massa atômica é
definida como sendo exatamente um dozeavos da massa de um átomo
de carbono 12. Em outras palavras, a massa de um átomo de
carbono 12 é, por definição, exatamente 12 u.
Em termos numéricos:
1u = 1,6605 x 10-27kg
A massa de um átomo de carbono 12 vale:
m(C) = 12 ( 1,6605 x 10-27
kg ) = 1,9926 x 10-26 kg
e esse valor inclui as massas dos prótons, nêutrons e elétrons.
A massa de um elétron é:
m(e) = 9,1093 x 10-31
kg
de modo que a massa dos 12 elétrons do átomo de carbono 12 é:
m(12e) = 12 ( 9,1093 x 10-31
kg ) = 1,0931 x 10-29 kg
Dessa forma:
m(C) / m(12e) = ( 1,9926 x 10-26
kg ) / ( 1,0931 x 10-29 kg
) = 1,8229 x 103
Assim, a massa dos elétrons é desprezível comparada à massa
do átomo e a massa do átomo pode ser considerada igual à massa
do núcleo atômico.
Em termos da unidade de massa atômica, as massas do próton
e do nêutron são, respectivamente:
m(p) = 1,0078 u
m(n) = 1,0087 u
Por outro lado, com os valores:
c = 2,9979 x 108 m/s
1J = 6,2415 x 1012 MeV
para o módulo da velocidade da luz no vácuo e para a relação
entre J e MeV, vem:
uc2 = 931,4815 MeV
m(e)c2 = 0,5110 MeV
m(p)c2 = 938,7471 MeV
m(n)c2 = 939,5854 MeV
Isótopos
Isótopos são núcleos associados ao mesmo elemento da tabela
periódica (mesmo número atômico), mas com diferentes números de
nêutrons.
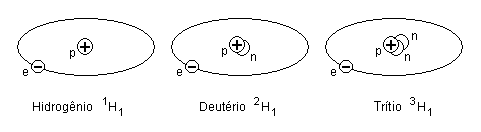
Por exemplo, ao elemento hidrogênio (Z = 1) estão
associados isótopos com N = 0, N = 1 (deutério) e N = 2
(trítio), referidos, também, pelo número de massa: hidrogênio 1,
hidrogênio 2 e hidrogênio 3.
Aos 112 elementos conhecidos estão associados uns 270
isótopos estáveis e mais de 2.000 instáveis.
Isóbaros
Isóbaros são núcleos associados a elementos diferentes da
tabela periódica mas com iguais números de massa.
Por exemplo, os núcleos berílio 10 (Z = 4, N = 6), boro 10
(Z = 5,N = 5) e carbono 10 (Z = 6, N = 4) são núcleos isóbaros.
Simbologia
É usual representar o núcleo de número de massa A e número
atômico Z por AX Z ou, simplesmente, AX,
onde X é o símbolo do elemento correspondente.
Por exemplo, o núcleo oxigênio 17 é representado por
17O 8 ou, simplesmente, 17O.
O número de nêutrons N não precisa ser representado porque
N = A
- Z.
Tamanho
As técnicas mais importantes para a determinação do raio
nuclear são aquelas que incluem o espalhamento de nêutrons e
elétrons.
Como os nêutrons não têm carga elétrica, não são
influenciados pela interação coulombiana nem com os nêutrons nem
com os prótons do núcleo. Mas como são influenciados pela
interação nuclear tanto com os nêutrons quanto com os prótons do
núcleo, os nêutrons espalhados sondam a distribuição de massa do
núcleo.
Por outro lado, os elétrons não são influenciados pela
interação nuclear nem com os nêutrons nem com os prótons do
núcleo. Mas, como têm carga elétrica não nula, são influenciados
pela interação coulombiana com os prótons do núcleo e sondam,
assim, a distribuição de carga do núcleo.
O raio de um núcleo com número de massa A, suposto
esférico, é dado, com precisão considerável, por:
[1] R = ro A1/3
onde ro é um coeficiente empírico, o
mesmo para todos os núcleos, com ro = 1,4
fm para a distribuição de massa e ro =
1,2 fm para a distribuição de carga. Aqui se usa como unidade de
comprimento o fermi:
1fm = 10-15 m
Esses números indicam que a distribuição de massa nuclear
avança um pouco além da distribuição de carga.
Como o volume de uma esfera é dado por V = 4pR3
/ 3, o volume do núcleo pode ser escrito:
[2] V = 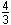 πro3
A
e a densidade da matéria nuclear fica:
[3] r = M / V = Au / ( 4πro3A
/ 3 ) = 3u /
πpro3
Em números:
r = 3 ( 1,6605 x 10-27
kg ) / 4p ( 1,4 x 10-15
m )3 = 1,4447 x 1017 kg / m3
A expressão [2] mostra que o volume nuclear é proporcional
ao número de núcleons. Assim, o número de núcleons por unidade
de volume é constante. Portanto, a densidade de núcleons é
constante. Ainda, o fator de proporcionalidade na expressão [2]
é o mesmo para todos os núcleos, de modo que a densidade de
núcleons é a mesma para todos os núcleos.
A massa de um próton é muito próxima da massa de um
nêutron. Então, não apenas a densidade de núcleons, mas também a
densidade de massa é constante e tem o mesmo valor para todos os
núcleos.
E mais, como a interação nuclear forte é independente da
carga elétrica, os prótons e os nêutrons estão distribuídos mais
ou menos uniformemente no núcleo e a densidade de carga também é
constante e tem o mesmo valor para todos os núcleos.
Na verdade, nos núcleos com número de massa A grande, a
densidade de carga na região central aparece diminuída devido à
repulsão coulombiana entre os prótons.
Um núcleo não tem, evidentemente, um raio exatamente
definido como se poderia inferir da expressão acima, nem uma
densidade constante no interior da esfera definida por esse
raio.
Na verdade, a densidade nuclear diminui até zero dentro de
um intervalo radial cujo centro é dado pela expressão
mencionada.
Por exemplo, para as distribuições de carga e de massa do
carbono 12:
Rc(C) = 1,2 ( 12 )1/3 fm
 2,7 fm
Rm(C) = 1,4 ( 12 )1/3 fm
3,2 fm
e do cobalto 59:
Rc(Co) = 1,2 ( 59 )1/3 fm
4,6 fm
Rm(Co) = 1,4 ( 59 )1/3 fm
5,4 fm
Assim, a uma distância do centro do núcleo de 2,7 fm para o
carbono 12 e de 4,6 fm para o cobalto 59, a densidade de carga
tem a metade do valor que atinge na região central.
As formas de alguns núcleos afastam-se
significativamente da forma esférica e devem ser consideradas
elipsoidais ou, mesmo, com a forma de uma pêra.
Física Nuclear
|
PORTAL
DE ESTUDOS EM QUÍMICA
FÍSICA
NUCLEAR