PROFESSOR

O que é ordem de reação?

O conceito de ordem de uma reação química está relacionado à expressão de velocidade. Ordem de reação é a soma dos expoentes aos quais estão elevadas as concentrações na expressão de velocidade, e não estão relacionados aos coeficientes estequiométricos.

Para a reação:

 

Teremos uma lei de velocidade:

  

Na qual:

 
 
 
E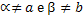 

A ordem de reação é determinada experimentalmente, no caso da cinética empírica, ou por meio de modelos matemáticos, a partir de dados espectroscópicos e de química teórica sobre as moléculas participantes, no caso da cinética química teórica. Na prática, as reações mais importantes são as de ordem zero, primeira e segunda ordens. Reações de terceira ordem são bastante raras e não são conhecidas reações de ordem superior a três.

Para conhecer a ordem de reação são necessários dados experimentais e hipóteses a respeito da seqüência de etapas elementares por meio das quais a reação ocorre, isto é, do mecanismo da reação.

Uma outra definição importante é a do conceito de molecularidade.  A molecularidade de uma reação é o número de espécies reagentes que tomam parte em uma etapa elementar da reação. Assim:

- molecularidade 1: apenas uma espécie química participa do processo de reação. Ex.: um rearranjo molecular.
- molecularidade 2: duas espécies químicas colidem entre si para que a reação ocorra.
- molecularidade 3: é muito rara, pois depende da ocorrência de uma colisão tripla. 

Enfim, é importante saber a diferença entre molecularidade e ordem:

- A ordem de uma reação é uma grandeza empírica, obtida a partir da lei de velocidade levantada experimentalmente.

- A molecularidade de uma reação é propriedade de uma reação elementar que faz parte de um mecanismo teórico de interpretação da reação.

Ordem Zero

Reações de ordem zero são reações em que a velocidade é uma constante, independente da concentração do reagente. São sempre reações não-elementares, como por exemplo, as reações fotoquímicas e as reações enzimáticas no início. 
Para uma reação de ordem zero, do tipo A → produtos, pode-se escrever:

 

Esta equação equivale a e é por isso que este tipo de reação é chamado de ordem zero.
Verifica-se que a constante de velocidade k para as reações de ordem zero tem unidades de [concentração] . [tempo-1]. Por exemplo:  
Integrando a equação, considerando-se conhecida a concentração no tempo t=0:

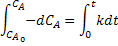
Obtém-se

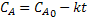
Verifica-se que a concentração do reagente diminui linearmente com o passar do tempo. Assim, o gráfico abaixo mostra como deve se comportar a concentração com o passar do tempo para uma reação de ordem zero.

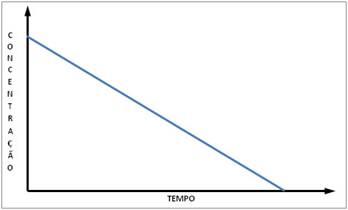
Este mesmo gráfico permite que se determine experimentalmente a constante de velocidade k da reação, pois k é o coeficente angular, ou inclinação da reta.

É possível fazer uma troca de variável, introduzindo-se o conceito de taxa de conversão, , que é definida como a fração de reagente já transformada em produtos em um determinado tempo de reação:

 

Isolando-se,  nesta equação, obtém-se:

 

E diferenciando-se em relação ao tempo:

 
  
Substituindo em  temos: 

      

E, integrando, vem:

 


  

 

Esta equação permite determinar o tempo necessário para se atingir uma certa conversão do reagente A.

Um conceito importante e bastante utilizado em cinética química é o de MEIA-VIDA. A meia-vida de uma reação é definida como sendo o tempo necessário para que a concentração do reagente diminua à metade de seu valor inicial.

A partir da equação acima pode-se obter a meia-vida de uma reação de ordem zero, pois quando transcorrer uma meia-vida, a concentração será igual à metade da inicial e, portanto, XA = 0,5, resultando:

 

e portanto:

  

Esta equação mostra que a meia-vida de uma reação de ordem zero é diretamente proporcional à concentração inicial do reagente.

Reações de Primeira Ordem

Uma reação de primeira ordem é aquela na qual a velocidade é diretamente proporcional à concentração do reagente. 

Para uma reação monomolecular, irreversível, de primeira ordem, ocorrendo a volume constante, do tipo A→produtos, tem-se:

 

Trata-se de uma reação de 1ª ordem, pois a concentração do reagente A encontra-se elevada ao expoente 1.
Nesta equação,  representa a velocidade de decomposição de A. 

Verifica-se que a constante de velocidade k para as reações de primeira ordem tem unidades de [tempo-1].
Separando as variáveis, a equação anterior pode ser integrada entre limites:

 

 

A partir desta equação, fazendo-se um gráfico de  em função do tempo, o coeficiente angular é o termo k, o que permite determinar experimentalmente a constante de velocidade da reação.

Na forma exponencial a equação acima fica:
 

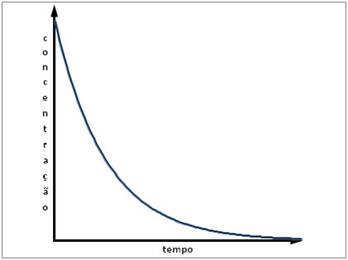
Esta equação mostra que a variação da concentração com o tempo para uma cinética de primeira ordem é exponencial, como representada no gráfico abaixo:

Utilizando-se aqui também o conceito de taxa de conversão: 

 

É possível isolar :

 

e

 

Pode-se então fazer uma troca de variáveis e escrever a equação 
 

 em função de :
 

Que pode ser dividida por , resultando:
 

Então, separa-se as variáveis e integra-se, obtendo-se:
 
 

Isolando t, se pode obter o valor do tempo necessário para atingir uma determinada conversão numa reação de primeira ordem:

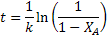
Meia-vida

Meia-vida é um conceito particularmente útil para as reações de primeira ordem, devido ao fato de estar relacionado diretamente com a constante de velocidade, dando uma idéia física da velocidade de reação melhor que a própria constante de velocidade.  Lembrando que a meia-vida de uma reação é o tempo necessário para que a concentração do reagente se reduza à metade do seu valor inicial e usando para uma reação de primeira ordem a equação 
 

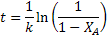
Quando , tem-se . Substituindo esse valor na equação acima, resulta:

 

Portanto a meia-vida de uma reação de primeira ordem é dada por:
 

Como se vê, a meia-vida de uma reação de primeira ordem é independente da concentração inicial do reagente. Este é o motivo pelo qual a meia-vida é utilizada, por exemplo, para caracterizar os isótopos radioativos. O decaimento radioativo é um processo nuclear que segue uma cinética de primeira ordem. Assim, uma tabela de nuclídeos apresenta os diferentes isótopos radioativos caracterizados por suas meias-vidas, que serão independentes das quantidades de núcleos radioativos presentes na amostra.

Reações de Segunda Ordem

Uma reação de segunda ordem é aquela onde há uma dependência da velocidade com o quadrado da concentração do reagente. Nas reações de segunda ordem, é preciso ter presente que elas podem ser monomoleculares ou bimoleculares. Para cada um desses casos, a equação diferencial resultante será diferente e eles devem ser tratados separadamente.

Reações de segunda ordem – primeiro caso:

No caso de reação monomolecular:
A→produtos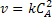             

Pode-se escrever então a seguinte equação diferencial:
 

Verifica-se que a constante de velocidade k para as reações de segunda ordem tem unidades de [concentração-1].[tempo^-1].

Separando as variáveis, a equação anterior pode ser integrada entre limites, resultando:

 

 

 

Esta é a equação de uma reta, quando se faz um gráfico do inverso da concentraçãoem função do tempo de reação. 

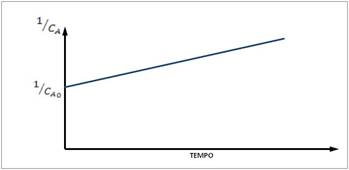
Deste modo, o coeficiente angular da reta obtida é k, o que permite determinar experimentalmente a constante de velocidade da reação.

Seguindo o método adotado anteriormente, exemplo, será introduzida a taxa de conversão .

 

Isolando-se :

 

E derivando em relação ao tempo:

 
Substituindo-se essas expressões em , tem-se:

 

Dividindo membro a membro por , resulta:

 

Separa-se então as variáveis desta equação:

 

Integrando:
 

E isolando t obtém-se o tempo necessário pra se atingir uma certa conversão do reagente A:

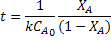
A meia-vida para esse tipo de reação é obtida fazendo =0,5 na equação anterior:

 

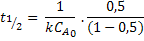
Essa expressão mostra que a meia-vida para uma reação monomolecular de segunda ordem é inversamente proporcional à concentração inicial do reagente.

Reações de segunda ordem – segundo caso:

No segundo caso, para reações bimoleculares de segunda ordem, pode-se representar a equação estequiométrica da seguinte forma:

aA+bB ® produtos
 

Nesse caso é necessário distinguir duas situações possíveis: a reação pode ser iniciada com a proporção estequiométrica dos reagentes ou com proporção não estequiométrica. Para cada uma destas situações a integração da equação diferencial resultante será diferente.

É importante destacar que os reagentes sempre irão reagir em proporção determinada pela estequiometria. No caso da reação aA+bB→produtos, independentemente da proporção inicial dos reagentes, sempre que a mols de A reagirem, b mols de B irão reagir para formar os produtos. Pode-se então escrever:

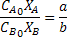
Partindo–se de proporções estequiométricas dos reagentes:

Para uma reação iniciada com a proporção estequiométrica dos reagentes, tem-se XA = XB e, portanto:

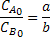
Para a reação aA+bB→produtos, pode-se escrever:
 

Ou, trocando as variáveis, para usar as taxas de conversão de A e de B:

 

Dividindo ambos os membros por , e observando que, para reações iniciadas com a proporção estequiométrica dos reagentes, :

 

Separando-se as variáveis, obtém-se:

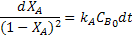
A integração desta equação resulta:

 

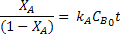
E isolando-se t:

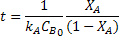
Note-se que, sendo utilizada a constante de velocidade , aparece na equação a concentração inicial . Por analogia pode-se obter a seguinte equação:

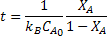
Partindo-se de proporções não estequiométricas dos reagentes:

Agora será analisado o caso em que a reaçãoaA+bB→produtos inicia com proporção não estequiométrica dos reagentes. Para essa reação pode-se escrever:

 

Considerando que os reagentes são sempre consumidos na proporção estequiométrica:
 

e portanto,

 

Substituindo este valor na equação , obtém-se:

 

Separando as variáveis e integrando (recomenda-se consultar uma tabela de integrais), resulta:

 

 

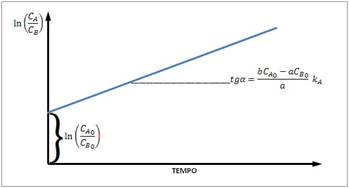
Substituindo os limites de integração e rearranjando chega-se a:

 

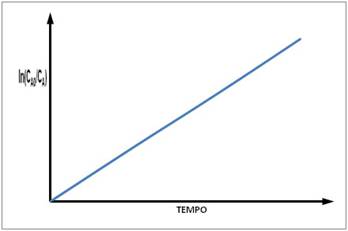
Esta é a equação de uma reta, de modo que fazendo-se um gráfico de ln(CA/CB) em função do tempo, temos como coeficiente angular o termo  , o que permite determinar experimentalmente a constante de velocidade da reação, pois as concentrações iniciais e são conhecidas, assim como os coeficientes estequiométricos a e b.

Home | Introdução | Leis da Velocidade | Ordens de Reação | Reações Reversíveis | Mecanismos das Reações | Exercícios | Bibliografia

Este site foi atualizado em 04/03/19